The Fibonacci sequence is a sequence in which each number is the sum of the two previous ones, starting with 0 and 1 as the base cases. A Fibonacci number is a number in the Fibonacci sequence. The golden ratio can be computed from the ratio between two Fibonacci numbers in consecutive sequence, as the sequence approaches infinity.
Here we will talk about how to compute the nth number in the Fibonacci sequence.
The Fibonacci sequence looks like: $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …$
Computing the nth Fibonacci number is a popular programming algorithm that can be easy to grasp but difficult to master, and this is why it often is found in programming interviews.
Recurrence Relation
The Fibonacci sequence is typically written as the recurrence relation f(n) = f(n-1) + f(n-2) but I recommend writing the base cases in the recurrence relation because it will translate better into code. Therefore a more complete recurrence relation:
$$ \begin{equation} f(n) = \begin{cases} 0 & \text{ n = 0 } \\ 1 & \text{ n = 1 } \\ f(n-1) + f(n-2) & \text{ n } \geq \text{ 2 } \end{cases} \end{equation} $$
Recursion
We can implement in C++ code from recurrence relation. A recurrence relation lends it self well for a recursive function.
The base cases of the recurrence relation are the base cases of the recursive function.
int fib(int n)
{
if ( n == 0 )
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
else
{
return fib(n-1) + fib(n-2);
}
}
Time complexity is O(2^n) because each call generates two recursive calls to the same function. Space complexity is O(n) because of recursive call stack, it goes as deep as the input n.
Dynamic Programming
We can do better than a basic recursive function by using dynamic programming. Dynamic Programming requires two things: optimal substructure and overlapping subproblems. Optimal substructure comes from the recurrence relation (e.g., f(n) = f(n-1) + f(n-2)). Overlapping subproblems can be seen from the recursion tree.
First, draw the recursion tree:
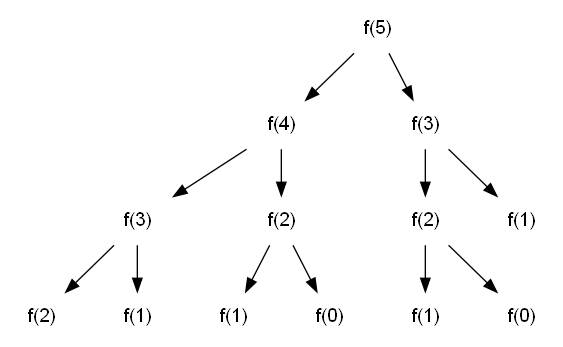
Next, identify the overlapping subproblems:
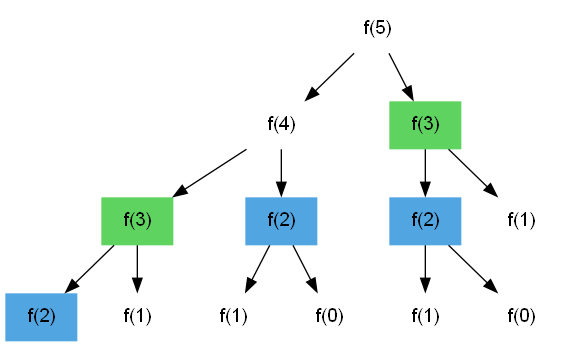
In this case f(3) and f(2) are repeated work. If we cache the result from f(3) on the first computation then we don’t need to recompute it. We can cache the results in an array.
When we have these two things we can use an array to cache our results.
Top-Down with Memoization
Essentially, because we have overlapping subproblems, we can cache the results of the recursive solution. This is referred to as a top-down approach.
int fib(int n)
{
if ( n == 0 )
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
vector<int> mem(n+1, -1);
mem[0] = 0;
mem[1] = 1;
return helper(n, mem);
}
int helper(int n, vector<int> & mem)
{
// invalid value, compute fib
if ( mem[n] == -1 )
{
mem[n] = helper(n-1, mem) + helper(n-2, mem);
}
return mem[n];
}
Time complexity is O(n), every n value is computed once, then cached. Space complexity is O(2n) for memoization and stack space.
Bottom-up with Tabulation
With top-down approach we call the value we want to compute, e.g., f(5), and we cache result as we go. With bottom-up approach, we can look back at the recurrence relation again and see if we can approach is from another direction, e.g., starting from f(0) and working our way up to f(5). We can look at the recurrence relation and see that the formula naturally works out in a bottom-up approach too.
Again we can cache the results in a similar way.
int fib(int n)
{
if ( n == 0 )
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
int dp[n+1];
dp[0] = 0;
dp[1] = 1;
for ( int i = 2; i <= n; ++i )
{
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
Time complexity is O(n) and space complexity is O(n) because of the dp cache.
Bottom-up with Iteration
Finally, we can look and see that as we compute f(4), we only need f(3) and f(2), and no values before it, so we don’t need to cache all the values from 0 to n. Thus we can have better space complexity.
int fib(int n)
{
if ( n == 0 )
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
int prev1 = 0; // dp[0]
int prev2 = 1; // dp[1]
int cur;
for ( int i = 2; i <= n; ++i )
{
cur = prev1 + prev2;
prev1 = prev2;
prev2 = cur;
}
return cur;
}
Time complexity is O(n) and space complexity is O(1).
Binet’s Formula
An alternative approach is to use Binet’s formula. However, this could be more difficult to derive to an optimal solution. Binet’s Formula has better time complexity but breaks down for large values of n.
//
int fib(int n)
{
if ( n == 0 )
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
constexpr double goldenRatio = (1.0 + sqrt(5)) / 2.0;
return (int) floor( pow(goldenRatio, n) / sqrt(5) + 0.5);
}
Time complexity is O(logn), pow function takes O(logn) time. Space is constant.
